Type_Conservative definition. More...

Collaboration diagram for Data_Type_Conservative:

pure subroutine, public	data_type_conservative::computestream (cons, beta, dh)
	Subroutine for computing new (n+1) stream function. More...

pure subroutine, public	data_type_conservative::computevorticity (cons, Re, beta, dh)
	Subroutine for computing new (n+1) vorticity. More...

pure type(type_conservative) function, public	data_type_conservative::computeresidual (cons, Re, dh)
	Function for computing residuals. More...

Detailed Description

Type_Conservative definition.

Function/Subroutine Documentation

pure subroutine, public data_type_conservative::computestream	(	type(type_conservative), dimension(0:,0:), intent(inout)	cons,
		real(r8p), intent(in)	beta,
		real(r8p), intent(in)	dh
	)

Subroutine for computing new (n+1) stream function.

The second order derivatives of the Laplacian operator of the stream function equation are approximated by means of second order central differences and then the resulting finite difference equation is solved by means of a Successive Over Relaxation (SOR) approach: 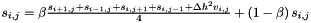$s_{i,j}=\beta\frac{s_{i+1,j}+s_{i-1,j}+s_{i,j+1}+s_{i,j-1}+\Delta h^2v_{i,j}}{4}+\left(1-\beta\right)s_{i,j}$

Parameters

[in,out]	cons	Conservative variables.
[in]	beta	Relaxation parameter.
[in]	dh	Space step.

Definition at line 110 of file Data_Type_Conservative.f90.

Referenced by dcs_simulate().

Here is the caller graph for this function:

pure subroutine, public data_type_conservative::computevorticity	(	type(type_conservative), dimension(0:,0:), intent(inout)	cons,
		real(r8p), intent(in)	Re,
		real(r8p), intent(in)	beta,
		real(r8p), intent(in)	dh
	)

Subroutine for computing new (n+1) vorticity.

The second order derivatives of the Laplacian operator and the first order ones of the RHS of the vorticity equation are approximated by means of second order central differences and then the resulting finite difference equation is solved by means of a Successive Over Relaxation (SOR) approach: $v_{i,j}=\beta\left[\frac{v_{i+1,j}+s_{i-1,j}+s_{i,j+1}+s_{i,j-1}}{4}+ Re\frac{\left(s_{i,j+1}-s_{i,j-1}\right)\left(v_{i+1,j}-v_{i-1,j}\right)- \left(s_{i+1,j}-s_{i-1,j}\right)\left(v_{i,j+1}-v_{i,j-1}\right)}{16}\right]+\left(1-\beta\right)v_{i,j}$

Note: For the implementation of the boundary conditions see T. Stortkuhl, C. Zenger and S. Zimmer.

Parameters

[in,out]	cons	Conservative variables.
[in]	re	Reynolds number.
[in]	beta	Relaxation parameter.
[in]	dh	Space step.

Definition at line 144 of file Data_Type_Conservative.f90.

Referenced by dcs_simulate().

Here is the caller graph for this function:

pure type(type_conservative) function, public data_type_conservative::computeresidual	(	type(type_conservative), dimension(0:,0:), intent(in)	cons,
		real(r8p), intent(in)	Re,
		real(r8p), intent(in)	dh
	)

Function for computing residuals.

Parameters

[in]	cons	Conservative variables.
[in]	re	Reynolds number.
[in]	dh	Space step.

Definition at line 217 of file Data_Type_Conservative.f90.

Referenced by dcs_simulate().

Here is the caller graph for this function: