DCS
a Driven-Cavity Open source Simulator code
 All Classes Files Functions Variables Groups Pages
Data Types
Lib_PDE
Interfaces

Partial Differential Equations solving library. More...

+ Collaboration diagram for Lib_PDE:

Data Types

interface  lib_pde::dudi_fv
 Function for computing first partial derivative by means of Finite Volumes approach (Green's theorem). More...
 

Detailed Description

Partial Differential Equations solving library.

Data Type Documentation

interface lib_pde::dudi_fv

Function for computing first partial derivative by means of Finite Volumes approach (Green's theorem).

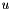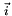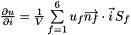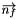Using the Green's theorem the first partial derivative of $u$ in $\vec i$ direction could be written as $\frac{{\partial u}}{{\partial i}} =\frac{1}{V}\sum\limits_{f = 1}^6 {{u_f}\overrightarrow {{n_f}} \cdot \vec i\,{S_f}}$ being $V$ the value of finite volume, $\overrightarrow {{n_f}}$ the outward unit normal of 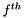$f^{th}$ face which area is $S_f$.

Note
It is assumed that the finite volume is discretized by means of a hexahedron.
Returns
fpd real variable.

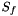Definition at line 121 of file Lib_PDE.f90.

Private Member Functions

pure real(r8p) function dudi_fv_r8 (u, nsi, v)
 Function for computing first partial derivative by means of Finite Volumes approach (Green's theorem). More...
 

Member Function/Subroutine Documentation

pure real(r8p) function lib_pde::dudi_fv::dudi_fv_r8 ( real(r8p), dimension(1:6), intent(in)  u,
real(r8p), dimension(1:6), intent(in)  nsi,
real(r8p), intent(in)  v 
)
private

Function for computing first partial derivative by means of Finite Volumes approach (Green's theorem).

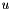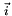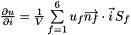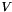Using the Green's theorem the first partial derivative of $u$ in $\vec i$ direction could be written as $\frac{{\partial u}}{{\partial i}} =\frac{1}{V}\sum\limits_{f = 1}^6 {{u_f}\overrightarrow {{n_f}} \cdot \vec i\,{S_f}}$ being $V$ the value of finite volume, 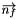$\overrightarrow {{n_f}}$ the outward unit normal of 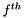$f^{th}$ face which area is $S_f$.

Note
It is assumed that the finite volume is discretized by means of a hexahedron.
Returns
fpd real(R8P) variable.
Parameters
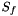[in]uValues of variable to be differentiated at each of 6 interfaces surrounding finite volume.
[in]nsiArea of 6 interfaces surrounding finite volume multiplied by normals projected along 'i'.
[in]vValue of finite volume.

Definition at line 135 of file Lib_PDE.f90.